Under the hood: Branch and Bound algorithm

General frame algorithm for solving discrete problems.

Brute force approach and enumeration of feasible solutions

We have seen in case of the festivals example, that brute force approach is a probably very slow, but valid approach to find an optimal solution when the search space is discrete and finite. Some acceleration ideas have also been mentioned, some of which may could be applied in a more general manner. Let's focus on enumerating only the feasible solutions now.

Enumerating all of the solutions was simple for the festivals, travesing through all of the subsets of a set is a simple task to do. We would only need to count from 0 to \(2^n-1\) and interpret the numbers binary representation as a subset indicator. Many of those subsets are, however, infeasible, and things get a little bit more difficult, if we want to generate the feasible solutions only. Try to figure out an approach to do so by yourself, or just click the button below. Show solution

There are many ways to do this, but a simple approach would be to follow these steps:

We wither go to F1 or not.

  1. If we don't go to F1, we wither go to F2 or not
    1. If we don't go to either F1 or F2, we can ither go to F3 or not
      1. If we don't go to F1,F2,F3, we have to go to F4 because that's the last option for Apocalyptica and Haggard
        1. If we go to F4, but not to F1, F2, or F3, we have to go to F5, as that is the last option for several bands.
          1. We go to F4 and F5, but not to F1,F2,F3. There are no decisions left, and we have a solution with 2 festivals.
      2. If we don't go to F1 or F2, but go to F3, we have to go F4 because that's the last option for Apocalyptica and Haggard
        1. If we go to F3 and F4, but not to F1 or F2, we wither go to F5 or not.
          1. If we go to F3 and F4, but not F1,F2 or F5, we have a solution with two festivals.
          2. If we go to F3,F4 and F5, but not F1 or F2, we have a solution with three festivals.
    2. If we go to F2, but not to F1, we can either go to F3 or not...
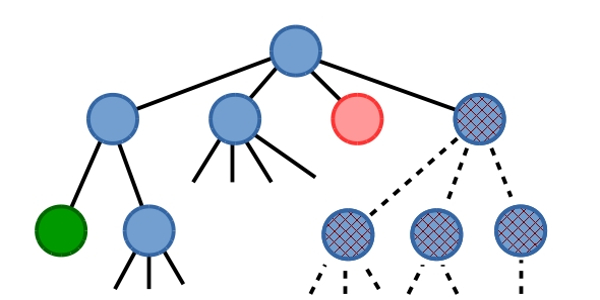
  2. If we go to F1, we wither go to F2 or not...

A tree-style enumeration of the feasible solutions can be observed in the above approach:

  • The root of the tree represents the case, when no decisions are made.
  • The leafs represent solutions, where all the decisions are made.
  • At each non-leaf node, a decision is made with all the possible outcomes "encoded" in its children.

Another way to look at the same tree is:

  • The root represents the set of all of the feasible solutions.
  • The leafs are single solutions, or more precisely: solution sets with a single element inside of them.
  • At each non-leaf node, a deacision is made, that divides the nodes' set into subsets, that will be its children.

The "Branch" part

The approach described above can be generalized to any problems with discrete decisions:

  1. Take the set of all of the feasible solutions, and assign them to the root node of a tree.
  2. For each tree node, whose set is not a singleton, select a decision, that has to be made, and parition the set assigned to that node so, that each subset contains the solutions having a specific outcome. Assign these subsets to children nodes. No children nodes are made for empty subsets.
  3. If the set of a node is a singleton, that node will be a leaf, and the solution can be evaluated

Note, that in general, Branch and Bound algorithms do not require the branching part to partition, i.e., to create disjoint subsets, only subsets, whose union covers the original set. Also, empty subsets may be represented and partitioned into further empty subsets, and singleton sets may be partitioned into empty sets and singleton sets, as reasoned below.

In practice, the sets assigned to nodes are usually not generated and partitioned explicitely. Instead, the outcomes of the former decisions are kept, and at each node it is somehow checked, whether:

These checks do not need to be 100% precise, however they must declare emptyness, singleton sets only with 100 percent certainty. This means, that it is ok, for the tester of "emptyness" to say "I'm not sure" on a set, and then treat it as a non-empty set, but it mustn't declare a set empty, if it is not. The same goes for identifying singletons.

If we already have the above branching algorithm, it can easily be extended with a minimum search on the leafs.

The "Bound" part

Let us consider a simple shortest path problem: I am currently living in Győr, and my parents live in Nagykanizsa. Let us assume, that I want to drive home the shortest way possible, only using main roads (roads with 1 and 2 digit numbers), but no highways to avoid additional fees.

This problem can obviously solved to optimality efficiently by e.g., Dijkstra's algorithm. Thus the presented approach here serves rather as an illustration, than as a recommendation for this particular problem class.

A simple way to split all of the feasible routes to subsets is to make a decision on the first part of my track, which can be either:

  1. Driving on road 1 to Mosonmagyaróvár
  2. Driving on road 85 to Csorna
  3. Driving on road 83 to Városlőd
  4. Driving on road 82 to Veszprém
  5. Driving on road 81 to Kisbér
  6. Driving on road 1 (in the other direction) to Komárom

A children node is created for all of these 6 options, and for example, the fourth node represents all of the solutions that start with Győr-Veszprém-.... For each node, branching can be done in the same fashion, for example, the route Győr-Veszprém can continue with:

We don't list the option of driving the road 82 back to Győr, as we are not interested in circular routes.

This can be repeated for all of the nodes, until we reach Nagykanizsa. If the "partial route" of a node ends at Nagykanizsa, it must be a leaf node, as that route is the only feasible solution with no circle that has that beginning. The length of the route can be evaluated and used in the minimum search.

This approach, however, is not very efficient. Assume, that we have already found the following leaf node: "Győr - Veszprém - Csopak - Balatonederics - Keszthely - Fenékpuszta - Balatonszentgyörgy - Nagykanizsa" with 217 km. When we find this solution, there may be other uninvestigated nodes with partial routes, for example: "Győr - Komárom - Budapest - Szolnok". If we were to blindly follow the instructions above, we would create two children nodes (branch this solution set into two) for following the direction towards either Jászberény or Törökszentmiklós.

We can, however, observe, that the route until Szolnok is already 227 km long, that is longer than a feasible solution we have found so far. Thus, there is no meaning in finding solutions in this subtree (in the set assigned to this node), as they will definitely be worse than a solution formerly found, hence not optimal. So, we can prune this node (solution subset) from the search, and look for another one.

What we did essentially is to give a lower bound on all of the solutions in that subtree (in the set assigned to the node), and if it was worse than the best solution found so far, the subtree (solution subset) was pruned. This idea can be generalized to any problem class, if there is a way to provide a lower bound on a subset of solutions. A general, pseudo-code like structure of the Branch-and-Bound frame algorithm looks like this:

  1. Set \(min\) to \(\infty\)
  2. Let \({\cal S}=\{ S \}\), where \(S\) is the set of all of the feasible solutions.
  3. While \(\cal S\) is not empty:
    1. Select and remove an element from \(\cal S\), and denote it with \(P\)
    2. If the lower bound on the solutions in \(P\) is greater than \(min\), then prune this set, and continue with another set from \(\cal S\) if there is one.
    3. Otherwise:
      1. If \(P\) is a singleton, chech the value of that solution, and update \(min\) if it is better than that.
      2. If \(P\) is not a singleton, find a decision that can further partition it, creating \(P_1,P_2,\dots\), then put the non-empty subsets into \(\cal S\)
  4. If \(min\) is not infinity, it has an optimal solution, and there is no feasible solution otherwise

Note, that this is a frame algorithm, that can be used for a lot of problem classes, where the details have to be specified, e.g.:

For example, we used the length of the "already traveled path" as the lower bound, and made branches based on the next segment in the path.

If the problem is maximization, we need to have an upper bound, and \(P\) is pruned if its bound is lower than the best solution so far (\(max\) in that case). Moreover, bound functions are usually required to give back the exact value of the solution contained in a singleton. If that is known about the bounding function, then no further conditional is needed to update \(min\) if \(P\) is a singleton, and its bound was already proven to be below \(min\).

Note about bounding functions

The "tightness" of a bounding function can be the most important contributor to the efficiency of an algorithm. If the bound is not tight, i.e., the bound is far from the actual value of the best solution in \(P\), then pruning will only happen deeper in the tree, and a subtree is investigated unnecessarily. To understand this, let's go back to our pruned path, "Győr - Komárom - Budapest - Szolnok". The parent of this node was "Győr - Komárom - Budapest", and it has 7 siblings. The bound of the parent is 126 km, which is way below of the 217 km long solution we have found earlier, so all 8 children nodes are generated. If we look at the map, we can see intuitievely, that this is really a wrong direction to go, as Budapest is east from Gyor, while Nagykanizsa is to the south-west. What this means, that just by looking at the map, we know, that none of the solutions in this subtree (in the set assigned to "Győr - Komárom - Budapest") will be better than the one we have already found. Still we need to generate the children, and in some cases the grandchildren to prove it, as our bound is not tight enough.

Our previous bound did not include anything about the distance, that is still to be traveled from the end of the current path. However, it is not difficult to provide a lower bound for that either. Simply we should add the geographical distance between the end of the current path and Nagykanizsa. For the "Győr - Komárom - Budapest" node, this Budapest-Nagykanizsa distance is 190 km. Adding the two together: 126 + 190 = 316 km, which is still a valid lower bound, as any "ending" of that path will be longer than 190 km. 316 km is way over 227, so with this tigther bound we can prune the "Győr - Komárom - Budapest" node, and we will not have to spend time generating and evaluating its children, grandchildren.

Note, that we can only prune "Győr - Komárom - Budapest", if we have a solution better than 316 km already. Thus, the strategy to explore the nodes in the tree can be just as important as a tight bound.

It seems, that we always have to strive towards tighter and tighter bounds to keep the B&B tree as small as possible. Tighter bounds, however, often require more complex calculations. A slightly tigther bound may not prune enough nodes to make up for the additional time spent on calculating that complex bound at each node. Selecting the best performing bound is not a trivial task, and is often done on a statistical basis.

Final notes

The purpose of this lecture is to provide a small insight about how the discrete part of an optimization problem is often handled by a solver.